P7: Accelerated Sampling Techniques
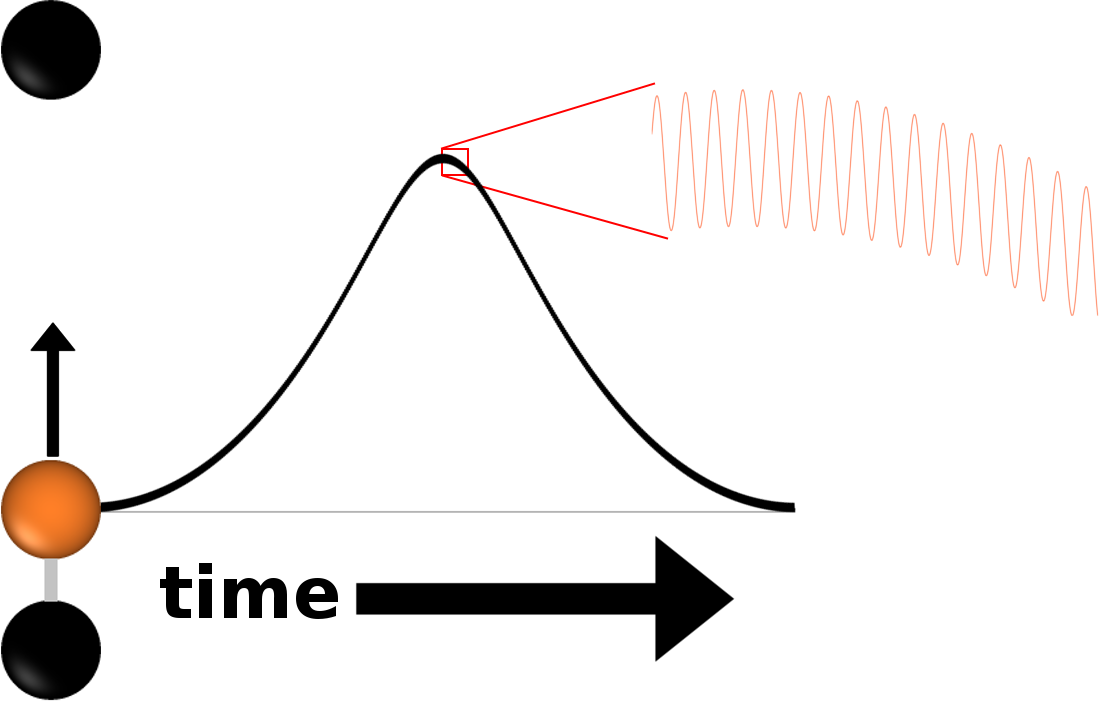
Molecular mechanics simulations are a ubiquitous tool in computational nanoscience. The workhorse technique in this field, the molecular dynamics approach, has been limited by the inherent short time-step required by the accurate discretization of Newton's equation of motion due to high-frequency oscillations in the solution. Since the range of applications is extremely broad there has been put a high emphasis on overcoming the stepsize restriction and ultimately accelerate the computation.
While the theory behind time integration of highly oscillatory ordinary differential equations is well known, long time step integration comes with its own set of challenges. One of the main tools in this field is geometric numerical integration. Under this common denominator falls a class of numerical integrators which aim to conserve certain geometric properties of the system. In our case the Hamiltonian, i.e. the energy, of the system. For the most part symplecticity was thought to be the driving factor behind energy conservation but when large timesteps come into play, the symmetry of the integrator becomes more relevant. We consider exponential integrators. For that, one first must think about a way to find a linearisation of the nonlinear bond potential, which has to be kept correct for the duration of the simulation. Second, the matrix function evaluations appearing in the trigonometric integrator must be calculated accurately and efficiently. Since the main goal is to beat the classic Störmer-Verlet method in computational speed, the driving factor, that must be employed in every step, is efficiency.
The aim of the project is to apply a certain extensively researched geometric numerical integrator to molecular dynamics. While doing so, the size of the largest possible stepsize increases, but so does the computational cost. We therefore want to implement the numerical scheme as efficient as possible, adapt it to the problem at hand and make it available to the RTG and other scientists in well-known molecular dynamics software.
Accelerated projects: